Assignment 1: Laser Escape Room
This assessment is intended for you to apply the mathematical skills you are learning in the first two weeks of the unit. It is also designed to practice working in groups and communicating your work clearly and precisely. These are all essential skills for your course and future career.
ENG1005 S2 Laser Escape Room Assignment University Australia.

General assignment rubric:
1.Electronic submission of this assignment is due on Moodle by 5pm on Monday 24 August 2020.
2.This assignment is not easy and it will not be doable if you leave it to the last minute. You will have covered what you need to get started by the end of week 1 and you could complete all of it by the end of week 2.
3.This is a group assignment. Only one member of the group is required to submit the assignment document.
4.Your assignment submission should include a description/explanation of what you are doing at each step and all relevant working. Without these your group will receive limited marks. The description should be in complete English sentences. All mathematics should be appropriately laid out and with appropriate notation. There are 2 additional marks given for the quality of the English, 2 additional marks for correct mathematical notation and 1 additional mark for appropriate sketches where relevant. These marks are easy to obtain but the markers will be instructed to be
strict in awarding these marks. Your writing should be similar in style to the typed lecture notes, not the shorter form of the videos and worked solutions. Further information on good writing style is posted on Moodle together with the assignments.
5.The solution should be a group effort, but each member of the group should write some portion of the final submission. You should clearly indicate who wrote what.
6.Handwritten assignments (or portions thereof) should be in blue or black ink and clearly legible. Solutions written on paper should be scanned and easily legible. For iOS, the default Notes app with the scan option (the camera icon at the bottom) works cleanly. For android,Cam Scanner is popular and has a free version. Many alternatives are also available.
7.The final document should be a single pdf file that is clearly and easily legible. If the marker is unable to read it (or any part of it) your group may lose marks.
8.Finally, there will be some peer assessment. The details of this are still being worked out and will be announced by the beginning of week 2.
You and your group have been trapped in a virtual escape room. All there is in the room is
- a laser in a fixed position on one wall,
- a mirror that can be moved around the room but whose orientation is fixed (i.e., its normal is always in the same direction) and
- a steel cable that holds the only door tightly shut.
All the walls of the room are vertical and are either mirrored or glass. All corners between walls are 90◦
You can fire the laser so that its beam reflects from mirrored surfaces and fries the cable holding the door shut. Your group can then escape. However, if the laser beam accidentally hits a glass wall, the glass shatters and the monster in the room next door can come after you. Your task is to carefully place the movable mirror in the room so that the laser beam hits the steel cable.
Here is a sketch of the room:
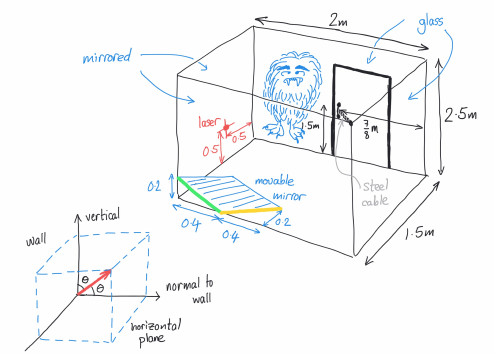
The laser points upwards and towards a mirrored wall, making an angle of cos−1(1/√3) ≈ 55◦ with both the normal to the wall on which it is mounted and the vertical (as shown above). The movable mirror is reflective on both sides and can be positioned at any location (including any height) in the room. Initially it is placed in the corner of the room, with one edge in contact with a mirrored wall (highlighted by a bold green line segment in the sketch above) and another edge in contact with the floor (highlighted by a bold yellow line segment in the sketch above).
Some information about mirrors:
(A) The physical laws for a mirror are that
– the reflected light ray is in the same plane as the incoming ray and the normal to the mirror
– the angle between the reflected ray and the normal to the mirror is the same as that between the the incoming ray and the normal to the mirror (usually stated as “the angle of reflection is equal to the angle of incidence”)
(B) The formula for the reflection of a vector a in a plane with normal n is a − 2(nˆ · a)nˆ.
The following questions will help guide you to finding an appropriate place for the mirror.
1.Describe the coordinate system that you will use. Your coordinate system should be right-handed. Where is the origin? How are the axes aligned? You may find it useful to include a sketch of the coordinate system, but you should also give some description in sentences.
2.In your coordinate system, write down a vector representing the direction that the laser is pointing. [Hint: if your answer cannot be multiplied by a scalar to eliminate all square roots, then look closer.]
3.Write down a vector equation for the line representing the laser beam as it leaves the laser.
ENG1005 S2 Laser Escape Room Assignment University Australia.

4.At what point does the laser beam hit a mirrored wall?
5.The laser light reflects perfectly off the mirrored wall. Write down a vector representing the direction that the laser beam points after reflection.
6.Now write down a vector equation for the line representing the reflected laser beam.
7.Find two vectors in the plane of the movable mirror and hence find a normal to the mirror. Regardless of the location of this mirror, this will always be its normal.
8.You will need to place this mirror somewhere along the path of the reflected laser beam to reflect it one more time. The beam reflects according to the description given above. Show that the formula in point
(B) obeys the physical laws in point (A). Then use the formula to write down a vector representing the direction of the reflected laser beam.
9.Now write down an equation for the line representing the twice-reflected laser beam. This will have two unknown parameters.
10.The laser beam should now be able to hit the steel cable. Write down a vector equation for the line representing the steel cable and hence write down a system of three linear equations to solve so that the laser beam hits the cable.
11.What is the point at which the laser beam hits the movable mirror (assuming you don’t want to free the monster)?
ENG1005 S2 Laser Escape Room Assignment University Australia.

Some extension thoughts (no credit)
All of these measurements have some error: error in aligning the laser, aberrations in the mirror, errors in the dimensions and so on. If there is say a 2 ◦error in the angles given above and the steel cable is 1 cm thick, would your group be able to escape? How would you calculate this? (Note that you would be unlikely to do this calculation by hand, but in ENG1060 you will be learning all the tools to do this in Matlab.)



